Ordinal graphs and their \(C^*\)-algebras
arXiv, 2025
We consider Cuntz-Krieger algebras for a class of left-cancellative categories with a fibration into the ordinals.
arXiv, 2025
We consider Cuntz-Krieger algebras for a class of left-cancellative categories with a fibration into the ordinals.
arXiv, 2025
We study topological quivers \(Q\) admitting a free and proper action by a locally compact group \(G\) together with their associated \(C^*\)-algebras.
Published:
Topological quivers are a somewhat natural generalization of topological graphs, where we insist that edge space is additionally endowed with a family of Radon measures, indexed by the vertex space, satisfying some regularity conditions. In this series of talks, we aim to present the needed background material to understand what a topological quiver \(C^*\)-algebra is, as well as discuss some results we hope to generalize from Deaconu, Kumjian and Quigg in the topological graph setting. One of these main results being that a locally compact group acting freely and properly on a topological quiver induces a Morita equivalence between the reduced crossed product of the quiver \(C^*\)-algebra and the \(C^*\)-algebra of the corresponding ‘quotient quiver’.
Published:
In this talk we introduce Quantum mechanics from first principles. We illustrate how Stone’s theorem and the Stone-von Neumann theorem bridge the gap between the canonical commutation relations for unbounded operators and the Weyl relations for unitary groups. Time permitting, we’ll recast the Stone-von Neumann theorem in terms of \(C^*\) crossed products and discuss how this motivates natural generalizations of the Stone-von Neumann theorem.
Published:
Topological quivers are a somewhat natural generalization of topological graphs, where we insist that edge space is additionally endowed with a family of Radon measures, indexed by the vertex space, satisfying some regularity conditions. In this series of talks, we aim to present the needed background material to understand what a topological quiver \(C^*\)-algebra is, as well as discuss some results we hope to generalize from Deaconu, Kumjian and Quigg in the topological graph setting. One of these main results being that a locally compact group acting freely and properly on a topological quiver induces a Morita equivalence between the reduced crossed product of the quiver \(C^*\)-algebra and the \(C^*\)-algebra of the corresponding ‘quotient quiver’.
Published:
We introduce a class of left-cancellative small categories for which there is a Cuntz-Krieger uniqueness theorem. The categories arise naturally as a generalization of directed graphs for which paths are allowed to have lengths which are ordinals. We will describe a collection of \(C^*\)-correspondences which generalize the usual correspondence for a directed graph. Under suitable conditions, these correspondences satisfy condition (S) of Eryüzlü and Tomforde, and we describe how a transfinite induction argument yields the uniqueness theorem.
Published:
We introduce a class of left-cancellative categories which generalizes the category of paths of a directed graph by allowing paths to have ordinal length. We use generators and relations to study the Cuntz-Krieger algebra defined by Spielberg. For each ordinal we construct an associated \(C^*\)-correspondence. Then we apply Eryüzlü and Tomforde’s condition (S) and obtain a Cuntz-Krieger uniqueness theorem for ordinal graphs.
Published:
We introduce a class of left-cancellative categories which generalizes the category of paths of a directed graph by allowing paths to have ordinal length. We use generators and relations to study the Cuntz-Krieger algebra defined by Spielberg. For each ordinal we construct an associated \(C^*\)-correspondence. Then we apply Eryüzlü and Tomforde’s condition (S) and obtain a Cuntz-Krieger uniqueness theorem for ordinal graphs.
Published:
We introduce a class of left-cancellative categories which generalizes the category of paths of a directed graph by allowing paths to have ordinal length. We use generators and relations to study the Cuntz-Krieger algebra defined by Spielberg. For each ordinal we construct an associated \(C^*\)-correspondence. Then we apply Eryüzlü and Tomforde’s condition (S) and obtain a Cuntz-Krieger uniqueness theorem for ordinal graphs.
Published:
We introduce a class of left-cancellative categories which generalizes the category of paths of a directed graph by allowing paths to have ordinal length. We use generators and relations to study the Cuntz-Krieger algebra defined by Spielberg. For each ordinal we construct an associated \(C^*\)-correspondence. Then we apply Eryüzlü and Tomforde’s condition (S) and obtain a Cuntz-Krieger uniqueness theorem for ordinal graphs.
Published:
We introduce a class of left-cancellative categories which generalizes the category of paths of a directed graph by allowing paths to have ordinal length. We use generators and relations to study the Cuntz-Krieger algebra defined by Spielberg. For each ordinal we construct an associated \(C^*\)-correspondence. Then we apply Eryüzlü and Tomforde’s condition (S) and obtain a Cuntz-Krieger uniqueness theorem for ordinal graphs.
Published:
We introduce a class of left-cancellative categories which generalizes the category of paths of a directed graph by allowing paths to have ordinal length. We use generators and relations to study the Cuntz-Krieger algebra defined by Spielberg. For each ordinal we construct an associated \(C^*\)-correspondence. Then we apply Eryüzlü and Tomforde’s condition (S) and obtain a Cuntz-Krieger uniqueness theorem for ordinal graphs.
Published:
I lectured on ideals and approximate units in \(C^*\)-algebras for GOALS 2025, which was held virtually. Here is a recording. Unfortunately zoom decided to cover half of the screen with the participants.
Published:
I lectured on universal \(C^*\)-algebras and graph \(C^*\)-algebras. Here is a recording. I learned from last time not to trust zoom, and I used my own recording software this time.
Published:
There is a certain class of ordinal graphs whose \(C^*\)-algebras are always Cuntz-Pimsner algebras in a natural way. In these examples, homomorphisms from algebras of distinguished subcategories into the ordinal graph algebra are injective. We will discuss this construction and some of the interesting details of the proof that these algebras are Cuntz-Pimsner algebras.
Published:
Abstract: We present criteria for when the \(C^*\)-algebra of an ordinal graph is naturally isomorphic to a Cuntz-Pimsner algebra. This condition also characterizes when certain homomorphisms from algebras of distinguished subcategories into the ordinal graph algebra are all simultaneously injective. We describe how an application of these results leads to a slight generalization of a previous Cuntz-Krieger uniqueness theorem.
Published:
Abstract: We consider \(C^*\)-algebras of categories we call ordinal graphs which generalize directed graphs by allowing paths to have ordinal length. We present criteria for when the \(C^*\)-algebra of an ordinal graph is naturally isomorphic to a Cuntz-Pimsner algebra. This condition also characterizes when certain homomorphisms from algebras of distinguished subcategories into the ordinal graph algebra are all simultaneously injective. We describe how an application of these results leads to a slight generalization of a previous Cuntz-Krieger uniqueness theorem.
Undergraduate course, Arizona State University, SoMSS, 2021
This was my first experience as a TA. I ran weekly review sessions, during which students completed practice problems, and graded the students’ homework.
Undergraduate course, Arizona State University, SoMSS, 2022
I ran weekly review sessions, during which students completed practice problems, and graded the students’ homework.
Undergraduate course, Arizona State University, SoMSS, 2022
This was my first experience as an instructor for a summer course. I was the sole instructor for this in-person course during the summer of 2022.
Undergraduate course, Arizona State University, SoMSS, 2022
I ran weekly review sessions, during which students completed practice problems, and graded the students’ homework.
Undergraduate course, Arizona State University, SoMSS, 2023
I ran weekly review sessions, during which students completed practice problems, and graded the students’ homework.
Undergraduate course, Arizona State University, SoMSS, 2023
I was the sole instructor for this in-person course during the summer of 2023.
Undergraduate course, Arizona State University, SoMSS, 2023
I was the sole instructor for this asynchronous online course during the summer of 2025.
Graduate course, Arizona State University, SoMSS, 2023
I ran weekly review sessions, during which the students and I practiced problems from past qualifying exams.
Graduate course, Arizona State University, SoMSS, 2023
I graded students’ homework and helped them prepare for the qualifying exam.
Undergraduate course, Arizona State University, SoMSS, 2024
I ran weekly review sessions, during which students completed practice problems, and graded the students’ homework.
Undergraduate course, Arizona State University, SoMSS, 2025
I ran weekly review sessions, during which students completed practice problems, and graded the students’ homework.
Last updated: February 25, 2021
Explore binary quadratic forms through Conway’s topographs. 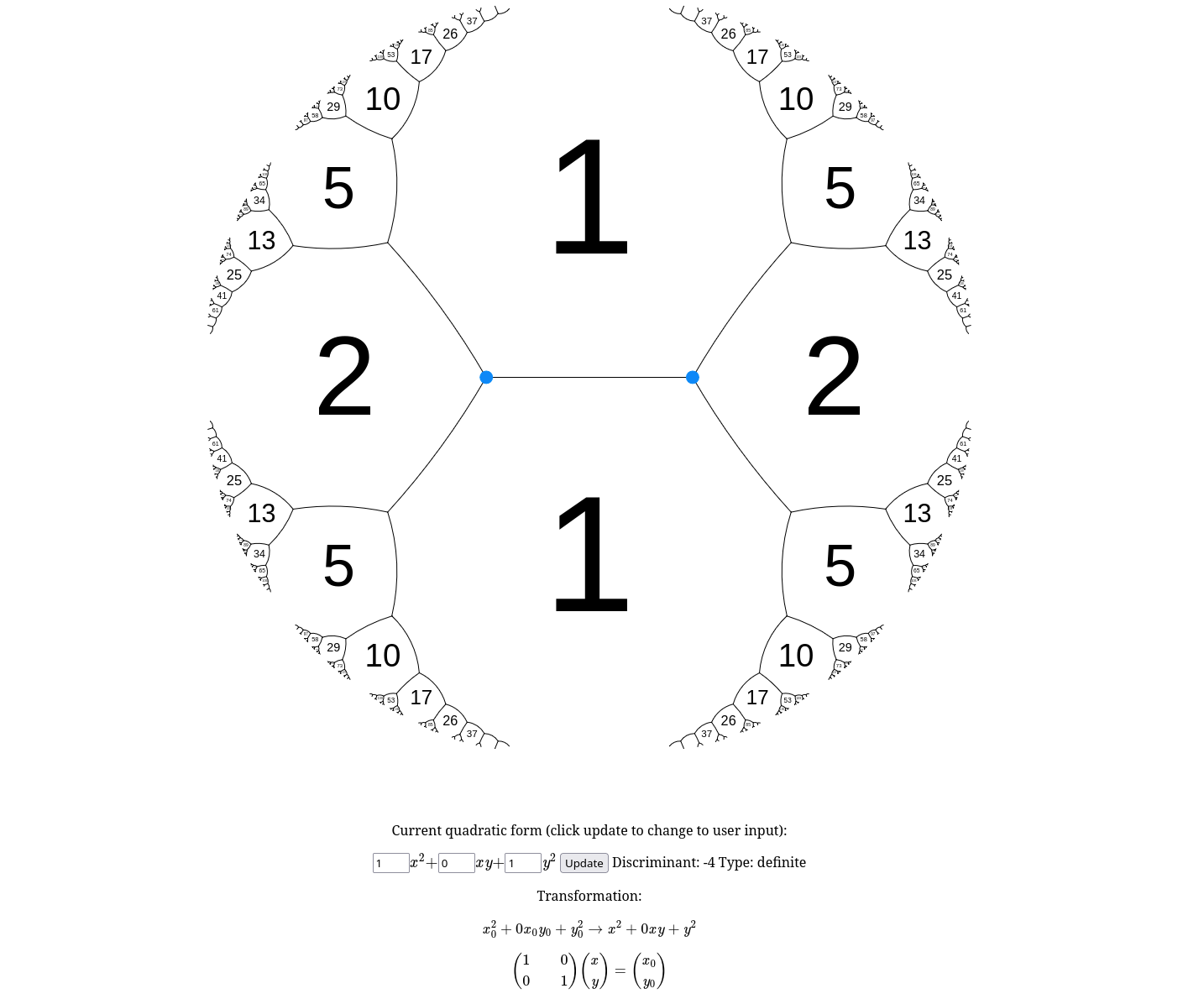
Last updated: December 04, 2024
I made pong, but the ball follows the rules of quantum mechanics. Click the link above to play!